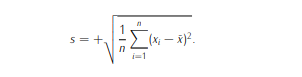La estadística descriptiva es un conjunto de técnicas numéricas y gráficas para describir y analizar un grupo de
datos, sin extraer conclusiones (inferencias) sobre la población a la que pertenecen. En este tema se introducirán
algunas técnicas descriptivas básicas, como la construcción de tablas de frecuencias, la elaboración de gráficas y
las principales medidas descriptivas de centralización, dispersión y forma que permitirán realizar la descripción
de datos.
Conceptos generales
En cualquier análisis estadístico el objetivo último es extraer conclusiones sobre un colectivo de interés denominada población. En ocasiones, el tamaño de la población (formada por individuos) puede hacer inabordable el estudio individualizado de las características de cada uno de ellos. Si se quisiera realizar un estudio sobre el nivel de glucemia en los varones adultos en España, sería imposible realizar una toma de glucemia en cada uno de ellos.
Para solucionar este problema, dichas mediciones se realizaran sobre una muestra.
Población: colectivo de individuos sobre los que se quiere extraer alguna conclusión.
Individuo: cada uno de los elementos de la población (unidad estadística).
Muestra: subconjunto (representativo) de la población, que se selecciona con el objetivo de extraer información.
Las técnicas de estadística descriptiva permiten describir y analizar un grupo dado de datos, sin extraer conclusiones (inferencias) sobre la población a la que pertenecen. Se tendrá que recurrir a la inferencia estadística, que
es la parte de la Estadística que trata las condiciones bajo las cuales las inferencias extraídas a partir de una
muestra son válidas, para extraer conclusiones sobre la población de interés.
Para aplicar una técnica descriptiva,
numérica o gráfica, será necesario analizar previamente el tipo de variable con la que se está trabajando.
Variable estadística: cada una de las características consideradas con el propósito de describir a cada
individuo de la muestra.
Tipos de variables: distinguiremos dos tipos de variables. Las variables cualitativas o categóricas (aquellas
que no se pueden expresar a través de una cantidad numérica) y las variables cuantitativas (se puede
expresar a través de un número).
A su vez, estas últimas pueden clasificarse en discretas y continuas, según
el tipo de valores que tomen. En el Cuadro 1 se incluyen algunos ejemplos
Distribuciones de frecuencias
Las tablas de frecuencias son una de las técnicas básicas para el resumen de información a partir de una muestra
de datos.
Su construcción es sencilla pero en conjuntos de datos de un tamaño moderado o grande su cálculo
puede resultar laborioso, aunque se pueden obtener utilizando cualquier paquete estadístico.
Tablas de frecuencias: las tablas de frecuencias se utilizan para representar la información contenida en
una muestra de tamaño n extraída de una población, (x1, . . . , xn).
Modalidades: cada uno de los valores que puede tomar una variable (cualitativa o cuantitativa discreta).
Se denotan como: ci
, i = 1, . . . , k.
El número de individuos de la muestra en cada modalidad ci se denota por ni
.
Frecuencia absoluta: para cada modalidad ci
, la frecuencia absoluta es ni
, i = 1, . . . , k.
Frecuencia relativa: para cada modalidad ci
, la frecuencia relativa es fi = ni
/n, i = 1, . . . , k.
Frecuencia absoluta acumulada: la frecuencia absoluta acumulada de una modalidad ci es Ni =
Pi
j=1 nj =
n1 + . . . + ni
, i = 1, . . . , k.
Frecuencia relativa acumulada: la frecuencia relativa acumulada de una modalidad ci es Fi =
Pi
j=1 fj =
f1 + . . . + fi =
Ni
n
, i = 1, . . . , k.
Ejemplo
Para estos datos, podemos construir una tabla de frecuencias, calculando frecuencias absolutas y relativas, así
como las respectivas acumuladas. ¿Cuál es la proporción de individuos con grupo A en la muestra? ¿Y con grupo
A o B?
La clasificación de variables que se ha expuesto en la sección anterior, distinguiendo entre variables cualitativas y
cuantitativas (discretas y continuas) es de crucial importancia a la hora de construir representaciones gráficas. De
modo esquemático, se introducen las principales técnicas de representación para variables cualitativas, variables
cuantitativas discretas y cuantitativas continuas. En el caso de variables cuantitativas discretas, si tienen pocos
valores, se puede hacer uso de las representaciones descritas para variables cualitativas (diagramas de barras y
sectores). Si por el contrario toman muchos valores, entonces se pueden utilizar las representaciones para variables
cuantitativas continuas.
Para la representación de variables cualitativas se suelen utilizar el diagrama de barras
o el diagrama de sectores. Para construir un diagrama de barras, en el eje horizontal se representan las
categorías o modalidades de la variable que se quiere representar y se levantan barras de altura proporcional a la frecuencia de cada modalidad (absoluta o relativa). En el diagrama de sectores también
se representan las distintas modalidades y su frecuencia, de manera que el círculo se reparte de forma
proporcional a la frecuencia de cada modalidad. Algunos ejemplos de estas representaciones para datos de
participación en redes sociales en un grupo de 180 jóvenes se muestran en la Figura 1.

Además del diagrama de barras descrito para las variables cualitativas,
que también se puede utilizar para variables cuantitativas discretas, para la representación de este tipo
de variables se tiene el diagrama acumulativo de frecuencias. El diagrama acumulativo de frecuencias se
construye representando, para cada modalidad de la variable ci
, los puntos (ci
, Ni
) (o bien (ci
, Fi
)) y
uniéndolos con segmentos horizontales y verticales, de forma que se obtiene una función escalonada. Si
se utilizan las frecuencias relativas acumuladas, el valor máximo del diagrama acumulativo se alcanza en
el 1, mientras que si se construye con las frecuencias absolutas acumuladas, el máximo será el número de
datos de la muestra. Se muestran el diagrama de barras y el diagrama acumulativo de frecuencias para la
variable "número de hijos de una familia" en la Figura 2 .
En el caso de variables cuantitativas continuas, podemos construir el
polígono (acumulativo) de frecuencias, de igual modo que el diagrama acumulativo de frecuencias explicado para variables cuantitativas discretas, pero considerando las marcas de clase de cada intervalo
ei en la representación. Sin embargo, son más usuales otras representaciones como el histograma y el
diagrama de tallo y hojas.
El histograma equivale en cierto modo al diagrama de barras, pero en el caso continuo, de forma que las
barras aparecen contiguas. En el eje horizontal se representan los intervalos de clase de la variable, y sobre ellos se levantan barras de altura hi = ni
/ai
(o bien hi = fi
/ai
), donde ni es la frecuencia absoluta
de cada intervalo (fi es la frecuencia relativa) y ai es la amplitud del mismo. Si el histograma se construye
con frecuencias relativas, la suma de las áreas de las barras es igual a 1. El histograma da una idea clara
de la distribución de los datos, pero es muy sensible a la elección de los intervalos de clase (véase Figura
3, panel izquierdo).
El diagrama de tallo y hojas es una representación que permite observar los datos y que a la vez da una idea de
la distribución de los mismos. Primero se seleccionan el número de cifras significativas (tallo) que se colocan a la
izquierda, se traza una línea vertical y se incluyen al lado las cifras siguientes de cada dato observado (hojas).
Se puede ver un ejemplo de representación para el peso de 300 personas en la Figura 3. Si se gira el diagrama
de tallo y hojas 90o
en el sentido contrario a las agujas del reloj, se puede observar una forma muy similar a la
del histograma.
Las medidas de posición o localización nos indican el valor o valores alrededor de los cuales se sitúan los datos
observados. Distinguiremos medidas de localización de tendencia central (media, mediana y moda) y de tendencia
no central (cuartiles, deciles y percentiles).
Como medidas de posición de tendencia central se introducirán la media aritmética o media muestral, la mediana
y la moda. Estas medidas nos proporcionan valores alrededor de los cuales se distribuyen los datos observados
en la muestra.
Media aritmética Se define como:
El valor de la media no tiene porqué pertenecer al conjunto de posibles valores de la variable. Por ejemplo,
puede resultar que el número medio de hermanos de una muestra no sea un número entero.
Uno de los problemas que presenta la media es que no es una medida robusta, es decir, su valor se ve
influenciada por datos anormalmente altos o bajos. Los datos que difieren numéricamente de las demás
observaciones se denominan valores atípicos.
Algunas modificaciones para corregir la falta de robustez son
la media truncada y media recortada. En la media truncada, un porcentaje de los datos atípicos se elimina
del cálculo y para obtener una media recortada, estos valores atípicos se substituyen por el punto de corte,
es decir, el dato inmediatamente inferior a los que se eliminan, para datos altos, y el inmediatamente
superior para los datos bajos.
Otra modificación es la media ponderada en la cual se asigna distintos pesos a las observaciones. En la
media aritmética cada observación tiene una contribución de peso 1/n al valor de x. En la media ponderada,
cada observación tendrá una ponderación ωi
, de tal modo que Pn
i=1 ωi = 1.
Mediana
Si suponemos que los datos de la muestra están ordenados de menor a mayor, la mediana es
el valor hasta el cual se encuentran el 50 % de los casos. Por tanto, la mediana dejará la mitad de las
observaciones por debajo de su valor y la otra mitad por encima. Así, si la muestra consta de un número
impar de datos (n impar), la mediana será el dato central. Si el tamaño de la muestra n es par, entonces
se tomará como mediana la media de los dos datos centrales.
En el caso de tener la variable representada en una tabla de frecuencias, podemos definir el intervalo
mediano, que será aquel cuya frecuencia relativa acumulada en el extremo inferior es menor que 1/2 y en
el extremo superior mayor que 1/2. La mediana, a diferencia de la media, es una medida robusta ya que su valor se ve poco afectado por la
presencia de datos atípicos. Si de una muestra se obtienen la media y la mediana y sus valores difieren
sustancialmente, esto será indicativo de la presencia de datos atípicos.
Moda
Para variables discretas o cualitativas, la moda es el valor o valores que más se repiten. Esto implica
que la moda no tiene porqué ser única. Para variables cuantitativas continuas, el intervalo modal es aquel
con mayor frecuencia. La moda se denotará por Mo.
Si los datos se encuentran agrupados, se puede obtener el intervalo modal como aquel que tiene una mayor
frecuencia.
Medidas de posición de tendencia no central
Como medidas de posición de tendencia no central, introduciremos los cuartiles, deciles y percentiles.
Cuartiles.
Los cuartiles Q1, Q2 y Q3 dividen la muestra en cuatro partes iguales, de manera que por debajo
de Q1 tenemos el 25 % de los datos, entre Q1 y Q2 se encuentra otro 25 % y por encima de Q3 otro
25 %. La idea de dividir la muestra en partes iguales se puede generalizar a la construcción de los deciles
(d1, . . . , d9, dividen la muestra el 10 partes iguales) y los percentiles (p1, . . . , p99, dividen la muestra el
100 partes iguales).
En general, se define el cuantil de orden p (0 < p < 1) como el valor que deja por debajo (a lo sumo) np
observaciones (por tanto, n(p − 1) observaciones por encima). El cuantil p se denotará por qp.
Medidas de dispersión absolutas
Las medidas de posición o localización indican en torno a qué valores se sitúan los datos, pero para obtener una
descripción más precisa de los mismos, es necesario conocer cuál es la dispersión que presentan. Las medidas de
dispersión absolutas dependen de las unidades en las que se miden las observaciones, siendo las más conocidas
la varianza muestral y la desviación típica muestral, que no es más que la raíz cuadrada de la varianza muestral.
Varianza (s
2
) y desviación típica (s). La varianza, s
2
, se calcula como:
La varianza está medida en las unidades de los datos al cuadrado, por lo que no se puede comparar
directamente con las medidas de posición, por ejemplo, con la media. Para obtener una medida en las
unidades de los datos, se considera la desviación típica:
Dada una muestra x1, . . . , xn, si consideramos la media x¯ como medida de posición de tendencia central, se podría
pensar en medir la dispersión a través de las diferencias de los valores a la media: (xi−x¯), para todo i = 1, . . . , n.
Una forma de contabilizar todas estas diferencias sería a través de la suma: Pn
i=1(xi − x¯). Sin embargo, en este
caso es previsible que muestras grandes nos den valores altos de esta suma de diferencias, por la intervención
de un mayor número de datos. Para corregir el efecto del número de datos, se podría pasar a un promedio, de
manera que la dispersión se mediría a través de: 1
n
Pn
i=1(xi −x¯).
Por las propiedades de la media muestral, vimos
que la media de las diferencias con respecto a la media es nula, así que esta expresión siempre resultará cero.
En este caso, las diferencias positivas y negativas a la media se compensan, por lo que para hacerlas positivas
podríamos pensar en medir estas diferencias al cuadrado: (xi − x¯)
2
.
De este modo se obtiene la varianza.
La varianza tiene las siguientes propiedades, fáciles de deducir a partir de la definición.
- Toma valores no negativos, puesto que se trata de un promedio de valores no negativos (diferencias al
cuadrado).
- La varianza no es lineal.
Si consideramos los datos yi = axi + b, la varianza de los nuevos datos será
s
2
y = a
2
s
2
x
.
Es decir, la varianza no se ve afectada por traslaciones (sumar o restar una constante), pero sí
por los cambios de escala al multiplicar los valores por un factor.
Medidas de dispersión relativa
Las medidas de dispersión absolutas dependen de las unidades de los datos, por lo que no son adecuadas para
comparar variables. Una de las medidas de dispersión relativa (no depende de las unidades de los datos) mas
usual es el coeficiente de variación:
El coeficiente de variación permiten comparar variables aunque estas estén registradas en distintas unidades de
medida. También es de utilidad para comparar variables que, aunque de la misma magnitud, están en escalas
distintas. Por ejemplo, para comparar las longitudes del diámetro del tímpano (normalmente, entre 8 y 10 milímetros)
y de la columna vertebral (en centímetros), podríamos transformar todas las observaciones a la misma escala pero
seguramente la dispersión´(medida en desviación típica) que encontraríamos en las longitudes del diámetro del
tímpano sería prácticamente nula.
Medidas de forma
Consideraremos dos medidas que proporcionan una idea de la forma de cómo se distribuyen los datos. Su cálculo
no es tan sencillo como el de las medidas de posición y dispersión estudiadas y lo que nos interesa es su
interpretación.
Coeficiente de asimetría.
El coeficiente de asimetría de Fisher toma valor 0 cuando la distribución de los
datos es simétrica con respecto a la media. Valores positivos de este coeficiente indicarán la presencia
de asimetría positiva (más datos con valores superiores a la media), mientras que valores negativos son
indicativos de una asimetría negativa (más datos con valores inferiores a la media). Se calcula como:
Existen muchas situaciones que requieren el análisis combinado de dos ó más variables, debido a las posibles
relaciones entre ellas. Para variables cuantitativas (continuas), una forma de representar la dependencia entre
ellas es a través de la recta de regresión. En esta sección introduciremos las medidas características usuales en
este contexto (vector de medias y matriz de varianzas-covarianzas) y veremos cómo se construye una recta de
regresión.
Covarianza y correlación
Supongamos que tenemos una variable bidimensional (X, Y ) y que disponemos de las observaciones en una
muestra de tamaño n, {(xi
, yi
)}
n
i=1. Se denomina vector de medias al vector cuyas componentes son las medias
muestrales de las variables: (x, ¯ y¯).
Para representar la dispersión podemos considerar los valores de las varianzas de cada variable por separado,
es decir, s
2
x
y s
2
y
, pero quedaría sin resumir la variabilidad conjunta de ambas. Por eso debemos introducir la covarianza. La covarianza entre dos variables X e Y , que es una medida que indica la variabilidad conjunta de
X e Y . Se calcula como:
Covarianza y correlación
El signo de la covarianza proporciona información sobre el tipo de relación que puede existir entre las variables.
De este modo:
a) Si la relación entre las variables es directa, entonces Sxy > 0.
b) Si la relación entre las variables es inversa, entonces Sxy < 0.
c) Si no existe relación lineal entre las variables, entonces Sxy = 0.
Las parejas de datos datos (xi
, yi
) con i = 1, . . . , n, de las dos variables (X, Y ) (también llamada variable bidimensional), se pueden representar a partir de una nube de puntos o diagrama de dispersión.
Esta representación
gráfica se construye representando sobre un plano los valores de los puntos observados. En la Figura 5 podemos
ver dos ejemplos de relaciones entre variables. La covarianza de los datos de la izquierda es positiva, mientras
que la covarianza de los datos de la derecha es negativa. Así, diremos que la relación entre X e Y es directa
cuando valores altos de X se corresponden con valores altos de Y . La relación se dice que es inversa si valores
altos de X se corresponden con valores bajos de Y , o viceversa.
La covarianza está afectada por las unidades de medida de las variables, por lo que definiremos una medida
característica para explicar la relación lineal entre variables que sea adimensional: el coeficiente de correlación
lineal.
A partir de una muestra de datos {(xi
, yi
)}
n
i=1, el coeficiente de correlación lineal se calcula como:

donde Sxy es la covarianza muestral y sx
, sy son las respectivas desviaciones típicas muestrales.
El coeficiente de correlación lineal no tiene dimensiones y toma valores en [−1, 1]. Valores cercanos a 1 nos
indicarían una relación lineal directa, mientras que valores cercanos a -1 darían una relación lineal inversa. En la
práctica, si el coeficiente de correlación r = 0, esto indica que no existe relación lineal entre las variables, pero
podría ocurrir que entre ellas hubiese otro tipo de relación no lineal. Observa que r sólo cuantifica relaciones
lineales.
Cuando existe una relación lineal entre dos variables, podemos tratar de buscar un modelo que describa una en
función de otra. La regresión lineal simple consiste en aproximar los valores de una variable a partir de los de
otra utilizando una relación de tipo lineal. La recta de regresión de Y sobre X tendrá la siguiente expresión:
y = a + bx,
donde a representa la ordenada en el origen o intercepto y b es la pendiente (indica la razón de cambio en Y
cuando X varía en una unidad). Esta expresión nos dice que, cuando x = 0, entonces y = a. La variable X se
denomina variable explicativa o independiente, mientras que la variable Y será la variable respuesta, o variable
dependiente.
Método de Mínimos Cuadrados
En la práctica, a partir de los datos {(xi
, yi
)}
n
i=1 podremos calcular los valores de a y b. El objetivo será obtener
los valores a y b que nos proporcionen los residuos más pequeños. Los residuos son las diferencias entre los
valores observados de la variable respuesta yi y los valores que proporciona el ajuste yˆi = a + bxi y vienen
dados por:
Coeficiente de regresión.
Se denomina coeficiente de regresión a la pendiente (parámetro b) de la recta de regresión de Y sobre X. Este
coeficiente proporciona información sobre el comportamiento de la variable respuesta Y en función de la variable
explicativa X y tiene el mismo signo que la covarianza.
a) Si b > 0, al aumentar los valores de X también aumentan los valores de Y .
b) Si b < 0, al aumentar los valores de X, los valores de Y disminuyen.
Coeficiente de determinación
Una medida para determinar cómo de bueno es el ajuste del modelo es el coeficiente de determinación (r
2
) que
mide la proporción de variabilidad de Y que explica X a través de la recta de regresión.
El coeficiente de determinación es el cuadrado del coeficiente de correlación lineal, y toma valores entre 0 y 1. Si
r
2
toma valores próximos a 1, esto será indicativo de un buen ajuste. El coeficiente de determinación del modelo
de regresión lineal simple viene dado por:
El coeficiente de determinación, y por tanto, la variabilidad explicada por la recta de regresión de Y sobre X y
la de X sobre Y es el mismo